Paula Cerejeiras
Lax pairs and the inverse scattering transform in Clifford analysis
Lax pairs are a well-established tool for the study of instationary non-linear PDE’s. Basically, the nonlinear PDE arises as a compatibility condition between two linear operators which themselves constitute its Lax pair. Since Lax pairs are closely linked to spectral decompositions they are not easily obtainable in the context of Dirac operators due to the non-commutativity of the underlying algebraic structure. In this talk we propose a construction of Lax pairs related to Dirac operators. The main idea here is to substitute the classic approach by the so-called AKNS method. We will show that it is possible to obtain Lax pairs for linear differential operators with polynomially generalized Dirac operators as well as non-linear PDE’s in the context of Clifford analysis. Moreover, this opens the way to apply the method of Inverse Scattering Transform (IST) for higher dimensional PDE’s.
Milton Ferreira
Continuous wavelet transform on the unit ball
Recently it was developed the continuous wavelet transform on the upper sheet of the 2-hyperboloid by defining a class of suitable dilations on the hyperboloid through conic projection and by incorporating hyperbolic motions belonging to the proper Lorentz group ) "\small \inline \fn_cm SO_0(1,2))")
. The wavelet transform was proved to be invertible whenever wavelets satisfy a particular admissibility condition, which turns out to be a zero-mean condition.
In this talk we will show how to obtain similar results in the unit ball of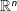 
. First we will define a class of radial dilation operators for the unit ball which will allow us to define together with motions on the unit ball the continuous wavelet transform. We study the admissibility condition for this transform in order to have admissible wavelets. For large radiuses of the ball the continuous wavelet transform on the ball match the usual continuous wavelet transform in .
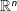Uwe Kähler
Discrete function theories in higher dimensions
In recent years one can observe an increasing interest in obtaining discrete counterparts for various continuous structures, especially in a discrete equivalent to continuous function theory. This is not only driven by the idea of creating numerical algorithms for different continuous methods of studying partial differential equations, but also for true discrete purposes, as can be seen, among others, by recent results of S. Smirnov in connecting complex discrete function theory with problems in probability and statistical physics or the introduction of finite element exterior calculus in analyzing variational crimes. While such ideas are very much developed in the complex case the higher-dimensional case is yet underdeveloped. This is mainly due to the fact that while discrete complex analysis is under (more or less) continuous development since the 1940’s discrete Clifford analysis started effectively only in the eighties and nineties with the construction of discrete Dirac operators either for numerical methods of partial differential equations or for quantized problems in physics. The development of Discrete Clifford analysis as being a discrete counterpart to classic Clifford analysis only started quite recently. In this talk we would like to present the necessary methods for constructing discrete function theories, review recent results as well as possible applications.
Ana Foulquié Moreno
On the full Kostant Toda system and the discrete Korteweg-de Vries equations
The relation between the solutions of the full Kostant-Toda lattice and the discrete Korteweg-de Vries equation is analyzed. A method for constructing solutions of these systems is given. As a consequence of the matricial interpretation of this method, the transform of Darboux is extended for general Hessenberg matrices.
This is a joint work with D. Barrios Rolanía and A. Branquinho.
This is a joint work with D. Barrios Rolanía and A. Branquinho.
